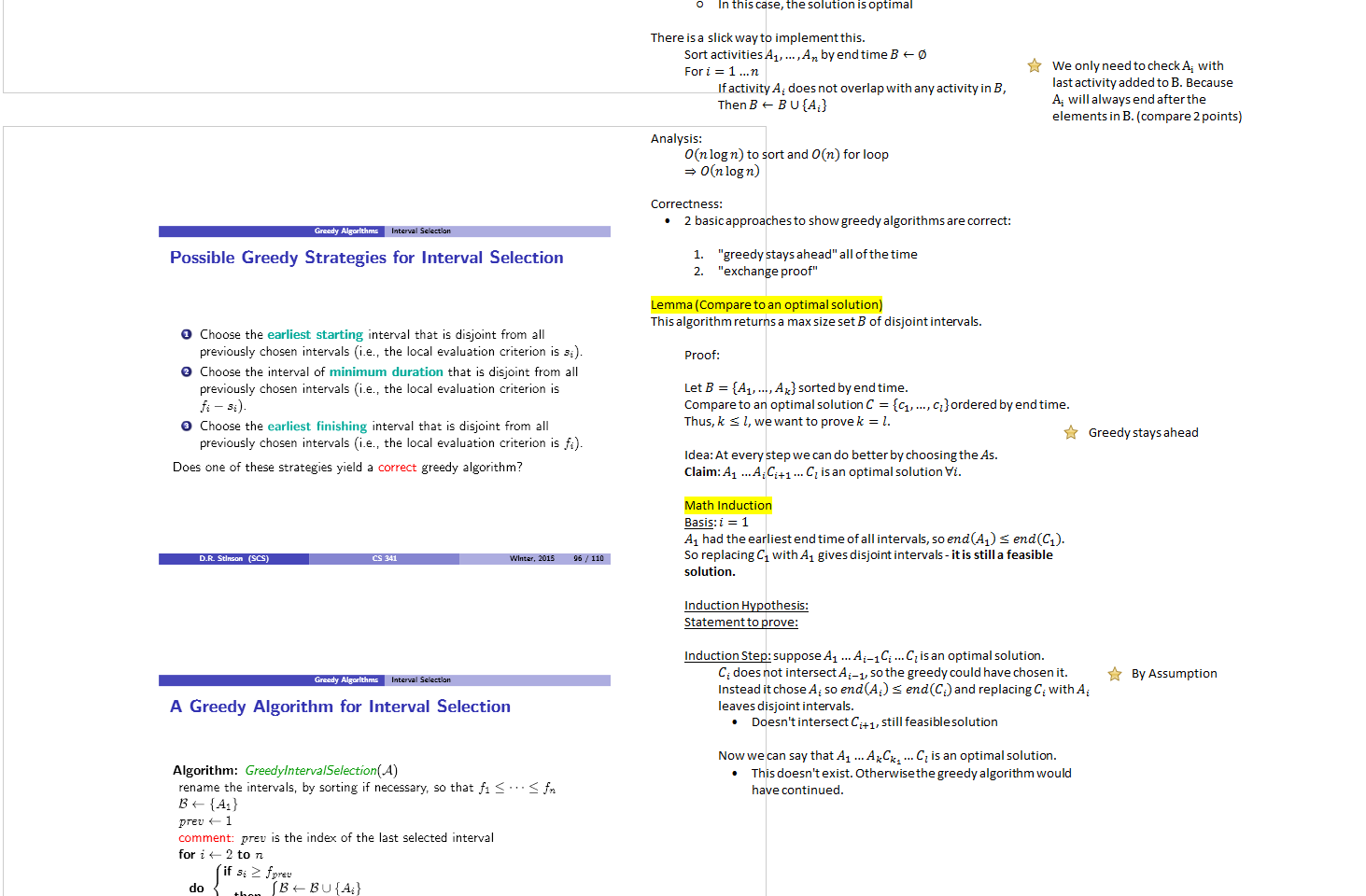
Greedy
Wednesday, May 27, 2015
9:02 AM
<<greedy.pdf>>
Inserted from: <file://\\psf\Dropbox\Schoolworks\Waterloo Terms\4B\CS431\greedy.pdf>


![Machine generated alternative text: I Dczlin Stratcr,
The Greedy Method
partial solutions
Given a problem instance I, it should be possible to write a
feasible solution X as a tuple [11,12.. .. x,] for some
integer ri, where r E X for all i. A tuple [xi,. . . ,x] where
i < n is a partial solution if no constraints are violated.
Note: it may be the case that a partial solution cannot be
extended to a feasible solution.
choice set
For a partial solution X = ra.. .. . xd where j < n, we
define the choice set
choice(X) = {y EX: [‘1..-. .x.y is a partial solution).
D.R. () Wtntar. 2015 fl/liD
“m D&,n Strateri
The Greedy Method (cont.)
local evaluation criterion
For any y e .1, g(y) is a local evaluation criterion that
measures the cost or profit of including y in a (partial)
solution.
extension
Given a partial solution X = [ri.... .Zj] where j < n,
choose y e choice(X) so that g(y) is as small (cx large) as
possible. Update X to be the (i± 1)-tuple [ri,... .Ii.y].
greedy algorithm
Starting with the “empty” partial solution, repeatedly extend
it until a feasible solution X is constructed. This feasible
solution may or may not be optimal.
WInw. 2015 03 ,‘ 110
D.R. SUman (SCS)](index_files/image003.png)













Greedy
Wednesday, May 27, 2015
9:02 AM
<<greedy.pdf>>
Inserted from: <file://\\psf\Dropbox\Schoolworks\Waterloo Terms\4B\CS431\greedy.pdf>


![Machine generated alternative text: I Dczlin Stratcr,
The Greedy Method
partial solutions
Given a problem instance I, it should be possible to write a
feasible solution X as a tuple [11,12.. .. x,] for some
integer ri, where r E X for all i. A tuple [xi,. . . ,x] where
i < n is a partial solution if no constraints are violated.
Note: it may be the case that a partial solution cannot be
extended to a feasible solution.
choice set
For a partial solution X = ra.. .. . xd where j < n, we
define the choice set
choice(X) = {y EX: [‘1..-. .x.y is a partial solution).
D.R. () Wtntar. 2015 fl/liD
“m D&,n Strateri
The Greedy Method (cont.)
local evaluation criterion
For any y e .1, g(y) is a local evaluation criterion that
measures the cost or profit of including y in a (partial)
solution.
extension
Given a partial solution X = [ri.... .Zj] where j < n,
choose y e choice(X) so that g(y) is as small (cx large) as
possible. Update X to be the (i± 1)-tuple [ri,... .Ii.y].
greedy algorithm
Starting with the “empty” partial solution, repeatedly extend
it until a feasible solution X is constructed. This feasible
solution may or may not be optimal.
WInw. 2015 03 ,‘ 110
D.R. SUman (SCS)](index_files/image003.png)
















Created with Microsoft OneNote 2010
One place for all your notes and information