Recall:

alphabet: finite set Σ of symbols

word: finite sequence of symbols over Σ

ε: empty string

language: set of strings over Σ

 

 How can we recognize automatically whether a given string belongs to a given language?

Answer: It depends on how complex the language is.

• {a2nb | n ≥ 0} – easy
• {valid MIPS assembly programs} – harder
• {valid Java programs} – harder
• some languages – impossible

 

Characterize languages according to how hard the recognition process is:  classes of languages based on difficulty of recognition.

• finite                                                easy
• regular                                                |
• context-free                                        | harder
• context-sensitive                                |
• recursive                                        v
• etc                                                impossible

 

Study high-level languages at as easy a class level as possible, move down when we have to.

 

Finite languages – have only finitely many words

• can recognize a word by comparing with each word in the (finite!) set.

 

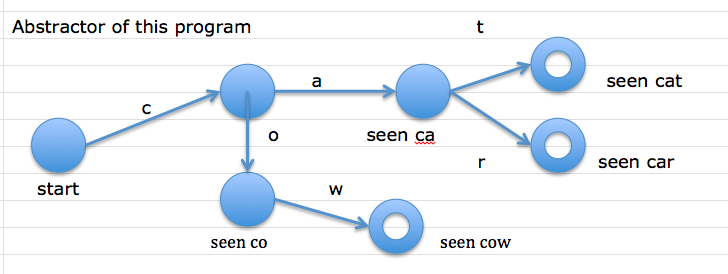
Exercise:

L = {cat, car, cow}

Write code to answer w ε L, such that: w is scanned exactly once, without storing previously-seen characters.

 

;scan input left-to-right if first char is c, move on, else reject if next char is a if next char is r if input is empty, accept, else reject else if next char is t if input is empty, accept, else reject else reject else if next char is 0 if next char is w if input is empty, accept, else reject else reject else reject

 



 

Bubbles are “states” – configurations of the program based on input seen.

 

Since programming languages don’t usually admit only finitely many programs, finite languages are not much use.

 

 Regular Languages

They are built from:

• finite languages
• union
• concatenation
• repetition

 

Union of two languages

• L1 ∨ L2 = {x | x ε L1 or x ε L2}

 

concatenation

• L1 Ÿ L2 = {xy | x ε L1, y ε L¬2}
• Ex:
• L1 = {dog, cat}
• L2 = {fish, ε}
• L1L2 = {dogfish, catfish, dog, cat}

 

repetition

• L* = {ε} union {xy | x ε L*, y ε L}
• 0 or more occurrences of a word in L
• {ε} U L U LL U LLL ….

 

Ex: L = {a, b}

• L* = {ε, a, b, aa, ab, ba…}

 

Show {a2nb | n >= 0} is regular

• ({aa})*Ÿ{b}

 

Shorthand-Regular Expressions

Expression	Language
	{} - empty language
aaa
	concat
	alteration (union)
	repetition

 

 Is C regular?

IDs = [a-zA-Z], ([a-zA-Z0-9_])*

 

A C program is a sequence of tokens. Each of which comes from a regular language.

C ⊆ {valid C tokens}*

So, maybe.

 

 How can we recognize an arbitrary regular language automatically?

Eg {a2nb | n >= 0}

.