Lec 25 - Sequences & Series
- Increasing: Proof by induction.
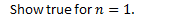
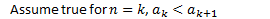

- Bounded: Proof by induction.
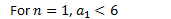
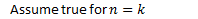

- To find the limit, take the limit of the formula.
Recall:
![]()
![]()
Definition
Increasing, decreasing, monotonic, bounded sequence.
![]() Aside: Completeness Axiom
Aside: Completeness Axiom
If a set of real numbers has an upper bound then there is a least upper bound.
![]() Theorem:
Monotonic Sequence Theorem
Theorem:
Monotonic Sequence Theorem
Every bounded, monotonic sequence is convergent.
Proof:
![]()
![]()
By the axiom above, if it is bounded there is a least upper bound.
![]()
![]()
![]()
![]()
![]()
![]()
This implies
![]()
Example
![]()
![]()
Proof:
![]()
Play with the sequence
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
…
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Taking the limit,
![]()
![]()
![]()
Therefore,
![]()
![]() Series
11.2
Series
11.2
Definition
An infinite series is an infinite sum of a sequence,
![]()
Definition
![]()
![]()
Definition
![]()
![]()
![]()
![]()
![]()
Definition
The geometric series is the sum of the geometric sequence.
![]()
![]()