Lec 8 - Reduced Row Echelon Form
Friday, January 20, 2012
9:31 AM
- No solutions
- One solution
- Infinite solutions
- Multiply a row by a non-zero number.
- Add multiple of a row to another row.
- Multiply a row by a non-zero scalar.
- Add a multiple of a row to another row.
- Swap two rows.
- All rows that have at least non-zero entry are above rows with only zeros.
- The leftmost non-zero entry in a row is a 1, called a leading one.
- The leading one in a row is to the right of the leading one in any row above it.
- Any column containing a leading one has it as its only non-zero entry.
Recall: We're trying to find solutions for the system of linear equations:
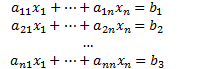
Either we have:
Definition
The set of all solutions of a system of linear equations is the solution set of the system.
Eg.
Solve the following system :
![]()
Add 4 times equation 1 to equation 2:
![]()
![]()
Divide equation 2 by 7:
![]()
![]()
Subtract 2 times equation 2 from equation 1:
![]()
![]()
Divide equation 1 by -1:
![]()
![]()
![]() Note:
For each operation we performed, we obtained a new system of linear equations
that had the exact same solution set.
Note:
For each operation we performed, we obtained a new system of linear equations
that had the exact same solution set.
Definition
If 2 systems of linear equations have the same solution set, then they are equivalent.
To solve a large system of linear equations, we will find equivalent systems that are easier to solve.
For each system, if we write the coefficients in order we don't need to write down the variables.
Definition
For the system of linear equations:
![]()
![]()
![]()
Is the coefficient matrix.
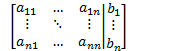
Is the augmented matrix.
Note: Rows represent equations and columns represent variables.

Eg
![]()
Has the coefficient matrix
![]()
And augmented matrix
![]()
We can apply the operations to solve this system to the augmented matrix.
Add 4 times equation 1 to equation 2:
![]()
Divide equation 2 by 7:
![]()
Subtract 2 times equation 2 from equation 1:
![]()
Divide equation 1 by -1:
![]()
![]()
![]() We
applied 2 basic operations:
We
applied 2 basic operations:
Sometimes, it may be help to switch the order of rows and this does not change the system.
Definition:
There are 3 elementary row operations (EROs) for solving a system of linear equations:
Applying EROs to a matrix is called row reducing a matrix.
If there is a sequence of EROs that transform one matrix to another, then the matrices are row equivalent.
![]() Theorem:
If augmented matrix are row equivalent, then the corresponding system of
linear equations are equivalent.
Theorem:
If augmented matrix are row equivalent, then the corresponding system of
linear equations are equivalent.
![]()
![]()
To find the solution for a given system, the augmented matrix needs to be row reduced to a form that makes it clear what the solution is.
Definition
A matrix is in reduced row echelon form (RREF) if:
![]()
Eg
![]()
![]()
![]() Theorem:
Every matrix has a unique RREF.
Theorem:
Every matrix has a unique RREF.