Lec 28 - Determinants

Wednesday, March 14, 2012

9:29 AM

    Recall:

    (Note: Every RREF matrix is upper triangular.)

     

    Question Q: What happens to the determinant of a matrix if we apply EROs to it?

     

    Important Theorem:

     

    Proof:

     

     

    Important Theorem:

     

    Proof:

    (only possible row swap)

     

     

     

     

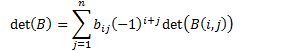
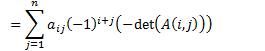
    (by inductive hypothesis)

     

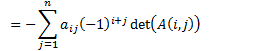
    Q.E.D.

     

     

    Important Theorem:

     

    Proof:

     

     

     

    Eg.

     

     

     

     

    Eg

     

     

     

     

     

     

     

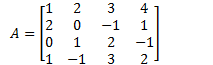
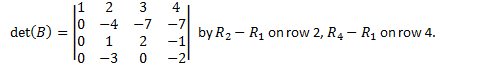
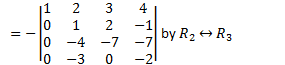
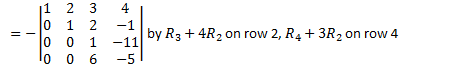
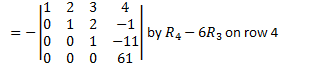
    Note: We can simulate an ERO by multiplying a matrix by an elementary matrix on the left.

     

    Important Theorem:

     

    Proof:

     

    Important Theorem (new property for the invertible Matrix Theorem):

     

     

 

Created by Tim Pei with Microsoft OneNote 2010
One place for all your notes and information