Lec 20 - Linear Independence & Basis

Friday, February 17, 2012

9:29 AM

     

    Important Linear Independence

     

    Definition

     

    Eg

     

    Solve the equation

    We get the following homogeneous system of linear equations:

     

     

    Row reduce the coefficient matrix:

     

     

     

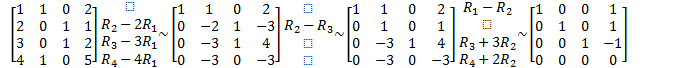
    Important Basis

     

    Question What is the smallest spanning set of a vector space?

     

    Important Theorem:

     

    Proof:

     

     

    Important Theorem

     

    Proof:

    Prove the contrapositive:

     

     

     

    Both theorems together imply the smallest spanning set of any vector space is linearly independent.

     

    Definition:

     

    Eg

     

    Eg

     

    This gives a system of linear equations:

     

    Row reduce the coefficient matrix:

     

     

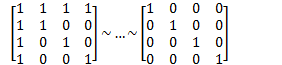
    Since the rank of coefficient matrix must equal to the number of columns, the homogeneous system has a unique solution (the trivial one).

     

     

     

     

 

Created by Tim Pei with Microsoft OneNote 2010
One place for all your notes and information