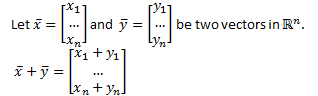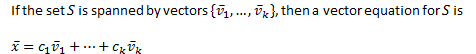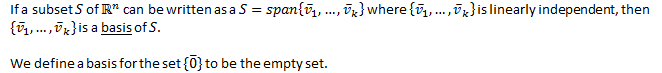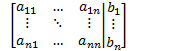Definitions and Theorems
Sunday, February 05, 2012
4:59 PM
|
Points
|
|
|
Vector addition |
|
|
Scalar multiplication |
|
|
Linear combination |
|
Theorem 1.1.1
![]()
|
Span Spanning set |
|
|
Vector Equation |
|
Theorem 1.1.2
![]()
|
Linearly Dependent Linearly Independent Trivial Solution |
|
Theorem 1.1.3
In order for a spanning set to be as small as possible, it must be linearly independent.
![]()
|
Basis |
|
|
Standard Basis |
|
|
|
|
|
K-plane |
|
|
|
|
|
|
|
Theorem 1.2.1
![]()
![]()
(Prove non-empty set, vector addition, and scalar multiplication)
Theorem 1.2.2
![]()
Theorem 1.3.1
![]()
![]()
|
Dot product |
|
Theorem 1.3.2
![]()
|
Length Norm |
|
|
Unit Vector |
|
Theorem 1.3.3 (Vector Properties)
![]()
|
|
|
|
Orthogonal |
|
|
Orthogonal set |
A set of vectors is an orthogonal set if every pair of vectors in the set is orthogonal.
|
|
Cross Product |
|
Theorem 1.3.4 (Properties of Cross Product)
![]()
|
|
|
|
|
|
|
Linear equation |
|
|
Coefficients |
|
|
System of linear equations |
(Note: A linear equation can be represented geometrically as a hyperplane.) |
|
Solution |
|
|
Consistent Inconsistent |
A system of linear equations is consistent if there is at least one solution. Otherwise it is inconsistent. |
Theorem 2.1.1
If the following system of linear equations:
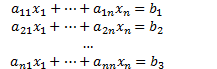
![]()
![]()
(A consistent system with more than one solution has infinitely many solutions.)
|
Solution set |
The set of all solutions of a system of linear equations is the solution set of the system. |
|
Equivalent |
If 2 systems of linear equations have the same solution set, then they are equivalent. |
|
Augmented Matrix |
For the system of linear equations:
Is the coefficient matrix.
Is the augmented matrix.
Note: Rows represent equations and columns represent variables.
|
|
Elementary row operations (EROs) |
There are 3 elementary row operations (EROs) for solving a system of linear equations:
|
|
Row reducing matrix |
Applying EROs to a matrix is called row reducing a matrix. |
|
Row equivalent |
If there is a sequence of EROs that transform one matrix to another, then the matrices are row equivalent. |
Theorem 2.2.1
If augmented matrix are row equivalent, then the corresponding system of linear equations are equivalent.
|
Reduced row echelon form (RREF) |
A matrix is in reduced row echelon form (RREF) if:
|
Theorem 2.2.2
Every matrix has a unique RREF.
|
Free variable |
|
|
Homogeneous system |
A system of linear equations is homogeneous if the RHS contains only zeros.
|
Theorem 2.2.3
![]()
|
Solution space |
The solution set of a homogeneous system is called the solution space of the system |
|
Rank |
The rank of a matrix is the number of leading ones in the RREF of the matrix.
|
Theorem 2.2.4
![]()