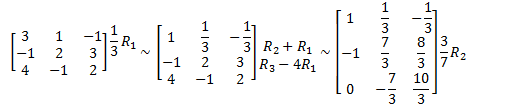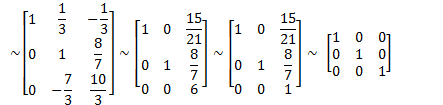Lec 9 - Echelon Reduce Operations

Monday, January 23, 2012

9:29 AM

Recall:

 

A matrix is in reduced row echelon form (RREF) if:

1. All rows that have at least non-zero entry are above rows with only zeros.
2. The leftmost non-zero entry in a row is a 1, called a leading one.
3. The leading one in a row is to the right of the leading one in any row above it.
4. Any column containing a leading one has it as its only non-zero entry.

(Note: Every Matrix has a UNIQUE RREF)

 

Eg

Solve







 



 



 



 

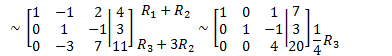
Represents







 

Solution is:



 

 

Eg

Solve

 







 



 



 



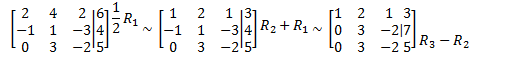
Since there is no choice of variables, this system is inconsistent.

 



 

 

Eg

Solve

 





 



 

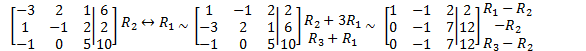
Represents:





 



 



 





 

The solution set of the system is



 





 

 

 

Definition:





 

 

Eg

Solve

 







 



 

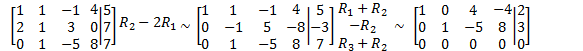
Let











 

The solution set is





 

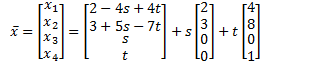
Eg



We must solve the system



 



 



 



 

 

 Homogeneous Systems

 

Definition

A system of linear equations is homogeneous if the RHS contains only zeros.



 



 

Note: Performing ERPs on a homogeneous system will not change the RHS. We just perform EROs on the coefficient matrix.

 

Eg

Solve